Introduction To Modern Cryptography 这本书英文原版的前两章笔记

Introduction To Modern Cryptography

Introduction and Classical Cryptography

Introduction

The Setting of Private-Key Encryption

• The syntax of encryption

  • message space: M​
  • three algorithms:
    • Gen
      • key space: K
    • Enc
    • Dec
  • for every key k​ output by Gen and every message $m\in M$, it holds that $Dec_k(Enc_k(m))=m$.

• Keys and Kerckhoff’s principle

  The cipher method must not be required to be secret, and it must be able to fall into the hands of the enemy without inconvenience.

  • It is significantly easier for the parties to maintain secrecy of a short key than to keep secret the algorithm they are using.
  • it will be much easier for them to change a key than to replace an encryption scheme.
  • for large-scale deployment it is significantly easier for users to all rely the same encryption algorithm.

Historical Ciphers and Their Cryptanalysis

• Caesar’s cipher: shift the letters of the alphabet

  • ROT-13 is still used nowadays, merely used to ensure the text is unintelligible.

• Sufficient key-space principle

  Any secure encryption scheme must have a key space that is sufficiently large to make an exhaustive-search attack infeasible.

  • this is only true if the message space is larger than the key space.

• The mono-alphabetic substitution cipher

  • attack relies on average letter frequencies
  • $\sum_{i=0}^{25}p_i^2\approx0.065=\sum_{i=0}^{25}p_i\cdot q_{i+j}$

• The Vigenere(poly-alphabetic shift) cipher

  • the character frequencies are “smoothed out”
  • attack: tabulate the frequency of each ciphertext character for each stream; Kasiski’ method; index of coincidence method

Principles pf Modern Cryptography

Principle 1 , Formal Definitions

• a threat model & a security goal

• An example: secure encryption

  • Wrong answers
    • it should be impossible for an attack to recover the key.
    • it should be impossible for an attack to recover the entire plaintext from the ciphertext.
    • it should be impossible for an attacker to recover any character of the plaintext from the ciphertext.
  • Right answer
    • regardless of any information an attacker already has, a ciphertext should leak no additional information about the underlying plaintext.

Principle 2 , Precise Assumption

• Reasons
  • mathematical proofs require this
  • Validation of assumptions
  • Comparison of schemes
  • Understanding the necessary assumptions

Principle 3 , Proofs of Security

Perfectly Secret Encryption

• Generating randomness:

  1. collect a “pool” of high-entropy data
  2. process the data to yield a sequence of nearly independent and unbiased bits

• rand() function in the C library is not cryptographically secure.

Definitions

• perfectly secret

  An encryption scheme with message space $M$ is perfectly secret if for every probability distribution over $M$, every message $m \in M$, and every ciphertext $c \in C$ for which $\Pr[C=c]>0$ :

  $\Pr[M=m|C=c]=\Pr[M=m]$

• an equivalent formulation of perfect secrecy

  For every $m,m\in M$, and every $c\in C$, $\Pr[Enc_K(m)=c]=\Pr[Enc_K(m')=c]$.

• The adversarial indistinguishability experiment $PrivK^{eav}_{A,\Pi}$

  1. The adversary $\mathcal{A}$ outputs a pair of messages $m_0,m_1\in M$.
  2. A key $k$ is generated using Gen, and a uniform bit $b\in \left\{0,1\right\}$ is chosen. Ciphertext $c \leftarrow Enc_k(m_b)$ is computed and given to $\mathcal{A}$. We refer to $c$ as the challenge ciphertext.
  3. $\mathcal{A}$ outputs a bit $b'$.
  4. The output of the experiment is defined to be 1 if $b'=b$, and 0 otherwise. We write $PrivK^{eav}_{\mathcal{A},\Pi}=1$ if the output of the experiment us 1 and in this case we say that $A$ succeeds.

• Perfectly indistinguishable

  Encryption scheme $\Pi=(Gen,Enc,Dec)$ with message space $M$ is perfectly indistinguishable if for every $\mathcal{A}$ it holds that $\Pr[PrivK_{\mathcal{A},\Pi}^{eav}=1]=\frac{1}{2}$

• Encryption scheme $\Pi$ is perfectly secret if and only if it is perfectly indistinguishable.

The One-Time Pad

• The one-time pad encryption scheme is perfectly secret.
  1. The key is as long as the message.
  2. The same key can be used only once.

Limitations of Perfect Secrecy

• If (Gen, Enc, Dec) is a perfectly secret encryption scheme with message space $M$ and key space $K$, then $|K| ≥ |M|$.

Shannon‘s Theorem*

• Shannon’s theorem

  Let (Gen,Enc,Dec) be an encryption scheme with message space $M$, for which $|M|=|K|=|C|$. The scheme is perfectly secret if and only if:

  1. Every key $k\in K$ is chosen with equal probability $1/|K|$ by algorithm Gen.
  2. For every $m\in M$ and every $c\in C$, there exists a unique key $k\in K$ such that $Enc_k(m)$ outputs c.

※：The theorem only applies` when $|M|=|K|=|C|$

Private-Key (Symmetric) Cryptography

Private-Key Encryption

Computational Security

• Computational security incorporates two relaxations relative to information theoretic notions of security
  1. Security is only guaranteed against efficient adversaries that run for some
     feasible amount of time.
  2. Adversaries can potentially succeed with some very small probability.

The Concrete Approach

• A scheme is $(t,\varepsilon)$-secure if any adversary running for time at most t succeeds in breaking the scheme with probability at most $\varepsilon$.

The Asymptotic Approach

• A scheme is secure if any ppt adversary succeeds in breaking the scheme with at most negligible probability.

• A function f from the natural numbers to the non-negative real numbers is negligible if for every positive polynomial $p$ there is an $N$ such that for all integers $n>N$ it holds that $f(n)<\frac{1}{p(n)}$.

  • $negl_1$ and $negl_2$ are negligible functions. Then,
    1. $negl_3(n)=negl_1(n)+negl_2(n)$ is negligible.
    2. $negl_4(n)=p(n)\cdot negl_1(n)$ is negligible.

Necessity of the Relaxations

• If we wish to encrypt many messages using a single short key, security can only be achieved if we limit the running time of the adversary.

Defining Computationally Secure Encryption

• A private-key encryption scheme is a tuple of probabilistic polynomial-time algorithm (Gen, Enc, Dec) such that:
  1. The Gen takes as input $1^n$ and outputs a key $k$; we write $k\leftarrow Gen(1^n)$. We assume without loss of generality that any key $k$ output by $Gen(1^n)$ satisfies $|k|\geq n$.
  2. The Enc takes as input a key $k$ and a plaintext message $m\in\left\{0,1\right\}^*$, and output a ciphertext $c$. Since Enc may be randomized, we write this as $c\leftarrow Enc_k(m)$.
  3. The Dec take as input a key $k$ and a ciphertext $c$, and outputs a message $m$ or an error. We assume that Dec is deterministic, and so write $m:=Dec_k(c)$. We denote a generic error by the symbol $\perp$ .

The adversarial indistinguishability experiment

1. The adversary $\mathcal{A}$ is given input $1^n$, and outputs a pair of messages $m_0,m_1$ with $|m_0|=|m_1|$.
2. A key $k$ is generated by running $Gen(1^n)$, and a uniform bit $b\in\left\{0,1\right\}$ is chosen. Ciphertext $c\leftarrow Enc_k(m_b)$ is computed and given to $A$. We refer to $c$ as the challenge ciphertext.
3. $A$ outputs a bit $b'$
4. The output of the experiment is defined to be 1 if $b'=b$, and 0 otherwise. If $PrivK^{eav}_{A,\Pi}(n)=1$, we say $\mathcal{A}$ succeeds.

Indistinguishable encryption in the presence of an eavesdropper/EAV-secure

• Definition 1: For all probabilistic polynomial-time adversaries $\mathcal{A}$ there is a negligible function $negl$ such that, for all $n$, $\Pr[PrivK_{\mathcal{A},\Pi}^{eav}(n)=1]\leq\frac{1}{2}+negl(n)$.
• Definition 2: For all PPT adversaries $\mathcal{A}$ there is a negligible $negl$ such that $|\Pr[out_{\mathcal{A}}(PrivK_{\mathcal{A},\Pi}^{eav}(n,0))=1]-\Pr[out_{\mathcal{A}}(PrivK_{\mathcal{A},\Pi}^{eav}(n,1))=1]|\leq negl(n)$

Encryption and Plaintext Length

• Sometimes leaking the plaintext length is problematic
  • Simple numeric/text data
  • Auto-suggestions
  • Database searches
  • Compressed data

Semantic Security*

• A private-key encryption scheme (Enc, Dec) is semantically secure in the presence of an eavesdropper if for every PPT algorithm $\mathcal{A}$ there exists a PPT algorithm $\mathcal{A}^{\prime}$ such that for any PPT algorithm Samp and polynomial-time computable functions $f$ and $h,$ the following is negligible:

  $\left|\operatorname{Pr}\left[\mathcal{A}\left(1^{n}, \operatorname{Enc}_{k}(m), h(m)\right)=f(m)\right]-\operatorname{Pr}\left[\mathcal{A}^{\prime}\left(1^{n},|m|, h(m)\right)=f(m)\right]\right|$

  where the first probability is taken over uniform $k \in\{0,1\}^{n}, m$ output by
  $\operatorname{Samp}\left(1^{n}\right),$ the randomness of $\mathcal{A},$ and the randomness of Enc, and the second probability is taken over $m$ output by $\operatorname{Samp}\left(1^{n}\right)$ and the randomness of $\mathcal{A}^{\prime}$.

• A private-key encryption scheme has indistinguishable encryptions in the presence of an eavesdropper if and only if it is semantically secure in the presence of an eavesdropper.

Constructing Secure Encryption Schemes

Pseudorandom Generators and Stream Ciphers

• For any efficient statistical test D, the probability that D returns 1 when given the output of the pseudorandom generator should be close to the probability that D returns 1 when given a uniform string of the same length.
• Pseudorandomness is computational relaxation of true randomness.
  • Considering only polynomial-time observers,a pseudorandom string is just as good as a uniform string.
• Let $l$ be a polynomial and let $G$ be a deterministic polynomial-time algorithm such that for any $n$ and any input $s\in\left\{0,1\right\}^n$ , the result $G(s)$ is a string of length $l(n)$. We say that $G$ is a pseudorandom generator if the following conditions hold:
  • (Expansion:) For every $n$ it holds that $l(n)>n$
  • (Pseudorandomness:) For any PPT algorithm $D$, there is a negligible function $negl$ such that $|\Pr[D(G(s))=1]-\Pr[D(r)=1]|\leq negl(n)$, where the first probability is taken over uniform choice of $s\in\left\{0,1\right\}^n$ and the randomness of $D$, and the second probability is taken over uniform choice of $r\in\left\{0,1\right\}^{l(n)}$ and the randomness of $D$.
    • We call $l$ the expansion of $G$.
• Stream Ciphers: (Init, GetBits)
  • Init
  • Input: seed $s$, optional initialization vector $IV$
  • Output: initial state $st_0$
  • GetBits
    • Input: state $st_i$
    • output： a block of several bits $y$, updated state $st_{i+1}$

Proofs by Reduction

• A security reduction is a particular type of mathematical proof that some cryptographic primitive or protocol is secure, in the sense that it is “at least as difficult to break” as some other problem believed to be hard.

• A proof that some cryptographic construction $\Pi$ is secure proceeds via the following steps:

  1. Fix some efficient adversary $\mathcal A$ attacking $\Pi$. Denote the $\mathcal A$ 's success probability by $\varepsilon(n)$.
  2. Construct an efficient algorithm $\mathcal A'$, called the “reduction”, that attempts to solve problem $X$ using $\mathcal A$ as a subroutine. And $\mathcal A'$ knows noting about how $\mathcal A$ works and only knows $\mathcal A$ is expecting to attack $\Pi$. So, given some input instance $x$ of $X$ , $\mathcal A'$ will simulate for $\mathcal A$ an instance of $\Pi$ such that:
     • (a) As far as $\mathcal A$ can tell, it is interacting with $\Pi$. That is, the view of $\mathcal A$ when run as a subroutine by $\mathcal A'$ should be distributed identically to the view of $A$ when it interacts with $\Pi$ itself.
     • (b) If $\mathcal A$ succeeds in “breaking” the instance of $\Pi$ that is being simulated by $\mathcal A'$, this should allow $\mathcal A'$, this should allow $\mathcal A'$ to solve the instance $x$ is was given, at least with inverse polynomial probability $1/p(n)$
  3. Taken together, (a) and (b) imply that $\mathcal A'$ solves $X$ with probability $\varepsilon(n)/p(n)$, if $\varepsilon(n)$ is not negligible. Moreover, if $\mathcal A$ is efficient then we obtain an efficient algorithm $\mathcal A'$ solving $X$ with non-negligible probability, contradicting the initial assumption.
  4. Given our assumption regarding $X$, we conclude that no efficient adversary $\mathcal A$ can succeed in breaking $\Pi$ with non-negligible probability. Stated differently , $\Pi$ is computationally secures.

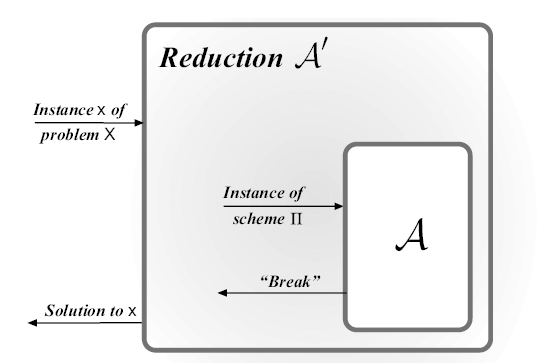
An instance for Reduction $\mathcal A'$——Distinguisher D

• D is given as input a string $\omega\in\left\{0,1\right\}^{l(n)}$.
  1. Run $\mathcal A(1^n)$ to obtain a pair of messages $m_0,m_1\in\left\{0,1\right\}^{l(n)}$
  2. Choose a uniform bit $b\in\left\{0,1\right\}$. Set $c:=\omega \oplus m_b$
  3. Give $c$ to $\mathcal A$ and obtain output $b'$, Output 1 if $b'=b$, and 0 otherwise.

Stronger Security Notions

Security for Multiple Encryptions

The multiple-message eavesdropping experiment $Priv_{\mathcal A,\Pi}^{mult}(n)$

1. The adversary $\mathcal A$ is given input $1^n$, and outputs a pair of equal-length lists of messages $M_0=(m_{0,1},\dots,m_{0,t})$ and $M_1=(m_{1,1},\dots,m_{1,t})$, with $|m_{0,i}|=|m_{1,i}|$ for all $i$.
2. A key $k$ is generated by running $Gen(1^n)$, and a uniform bit $b\in \left\{0,1\right\}$ is chosen. For all $i$, the ciphertext $c_i\leftarrow Enc_{k}(m_{b,i})$ is computed and the list $C=(c_1,\dots,c_t)$ is given to $\mathcal A$
3. $\mathcal A$ outputs a bit $b'$
4. The output of the experiment is defined to be 1 if $b=b'$, and 0 otherwise.

Indistinguishable multiple encryptions in the presence of an eavesdropper

• For all probabilistic polynomial-time adversaries there is a negligible function $negl$ such that $\Pr[Priv_{\mathcal A,\Pi}^{mult}(n)]\leq\frac{1}{2}+negl(n)$.

※：There is a private-key encryption scheme that has indistinguishable encryption in the presence of an eavesdropper, but not indistinguishable multiple encryption in the presence of an eavesdropper. For example: the encryption scheme is deterministic.

Chosen-Plaintext Attacks and CPA-Security

• encryption oracle: a “black box” that encrypts messages of $\mathcal A$’s choice using a key $k$ that is unknown to $\mathcal A$. $\mathcal A$ can interact with the oracle as many times ad it likes and query the reply of the oracle.

The CPA indistinguishability experiment $PrivK_{\mathcal A,\Pi}^{cpa}(n)$

1. A key $k$ is generated by running $Gen(1^n)$.

2. The adversary $\mathcal A$ is given input $1^n$ and oracle access to $Enc_k(·)$, and outputs a pair of messages $m_0, m_1$ of the same length.

3. A uniform bit $b\in\left\{0, 1\right\}$ is chosen, and then a ciphertext $c \leftarrow Enc_k(m_b)$ is computed and given to $\mathcal A$.

4. The adversary continues to have oracle access to $Enc_k(·)$, and outputs a bit $b'$.

5. The output of the experiment is defined to be 1 if $b' = b$, and 0 otherwise. In the former case, we say that $\mathcal A$ succeeds.

CPA-secure

• For all probabilistic polynomial-time adversaries $\mathcal A$ there is a negligible function $negl$ such that $\Pr[Priv_{\mathcal A,\Pi}^{cpa}(n)]\leq\frac{1}{2}+negl(n)$.

• Any private-key encryption scheme that is CPA-secure is also CPA-secure for multiple encryptions.

Constructing CPA-Secure Encryption Schemes

• Pseudorandom function: Let $F: \left\{0,1\right\}^*\times\left\{0,1\right\}^*\rightarrow \left\{0,1\right\}^*$be an efficient, length-preserving, keyed function. $F$ is a pseudorandom function if for all probabilistic polynomial-time distinguishers $D$, there is a negligible function $negl$ such that: $|\Pr[D^{F_K(\cdot)}(1^n)=1]-\Pr[D^{f(\cdot)}(1^n)=1]|\leq negl(n)$.

  • size: $|Func_n|=2^{n*2^n}$