算法备忘录·动态规划
本文最后更新于 2025年12月28日 晚上
一直以来,没能系统学习算法,是我心中的痛;现在学了 y 总的算法基础课,做做笔记,希望能够有所收获。
这是第六节,动态规划。
动态规划
闫氏 DP 分析法

背包问题
01 背包问题
- 问题: 个物品,每个物品的体积是 ,价值是 ,背包的容量是 。若每个物品最多只能装一个,且不能超过背包容量,则背包的最大价值是多少?
- DP 分析
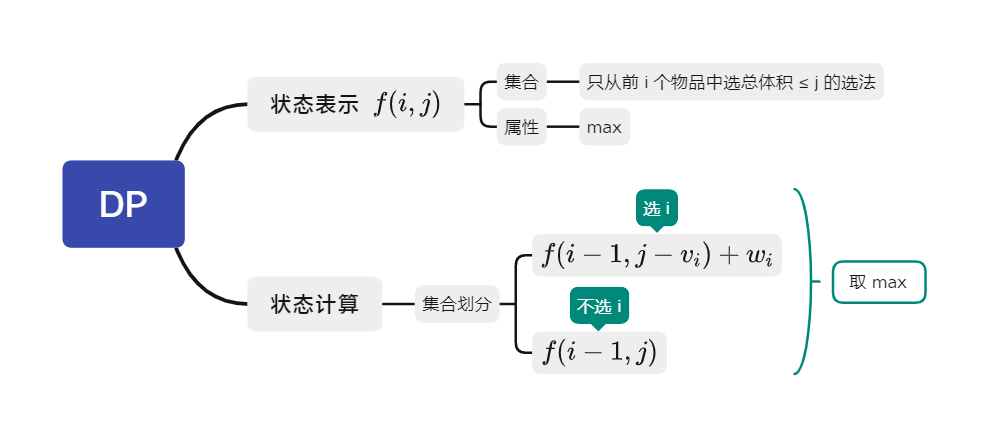
-
模板
- 二维形式
1
2
3
4
5
6
7
8
9
10
11
12
13int n; // 物品总数
int m; // 背包容量
int v[N]; // 重量
int w[N]; // 价值
int f[N][M]; // f[i][j] 表示 在考虑前 i 个物品后,背包容量为 j 条件下的 max 价值
for (int i = 1; i <= n; i ++ )// 从 1 开始是因为 i 为 0 时,f 一定为 0
for (int j = 1; j <= m; j ++ )
if (j < v[i]) f[i][j] = f[i - 1][j]; // 当前重量装不进
else f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
cout << f[n][m];- 利用滚动数组的原理转化为一维形式
1
2
3
4
5
6
7int f、[M];
for (int i = 1; i <= n; i ++ )
for (int j = m; j >= v[i]; j -- ) // 注意是倒序
f[i][j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m];
完全背包问题
- 问题: 个物品,每个物品的体积是 ,价值是 ,背包的容量是 。若每个物品有任意多个,且不能超过背包容量,则背包的最大价值是多少?
- DP 分析(优化后)

-
模板
- 未优化
1
2
3
4
5
6
7
8
9
10
11
12
13int n; // 物品总数
int m; // 背包容量
int v[N]; // 重量
int w[N]; // 价值
int f[N][M];
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
for (int k = 0; k *v[i] <= j; k ++ )
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k* w[i]);
cout << f[n][m];- 优化后(公式推出)
1
2
3
4
5
6
7
8int f[N][M];
for (int i = 1; i <= n; i ++ )
for(int j = 1; j <= m; j ++ )
if (j < v[i]) f[i][j] = f[j - 1][j];
else f[i][j] = max(f[i -1][j], f[i][j - v[i]] + w[i]); // 注意!这里和 01 背包的脚标有区别
cout << f[n][m] -
类似于 01 背包,也能转换为一维形式
1
2
3
4
5
6
7int f[M];
for (int i = 1; i <= n; i ++ )
for(int j = v[i]; j <= m; j ++ )
f[j] = max(f[j], f[j - v[i]] + w[i]); // 仍然是正序!
cout << f[m]
多重背包问题
- 问题: 个物品,每个物品的体积是 ,价值是 ,背包的容量是 。若每个物品至多装 个,且不能超过背包容量,则背包的最大价值是多少?
- 思路:多重背包问题不能像完全背包问题那样基于公式优化。它的优化思路是二进制优化——对于有 件的物品 ,可以打包为 个物品,每包有 件物品 ,其中 。这样,就转换为了 01 背包问题。
- 时间复杂度
- 模板
1 | |
分组背包问题
- 问题: 个物品,每个物品的体积是 ,价值是 ,背包的容量是 。若每组物品最多只能装一个,且不能超过背包容量,则背包的最大价值是多少?
- 思路:带有约束的 01 背包问题,递推方程
- 模板
1 | |
线性 DP
- 线性 DP:状态之间有线性关系的动态规划问题
- 没有比较固定的模板
数字三角形
- T:898. 数字三角形
- DP 分析:
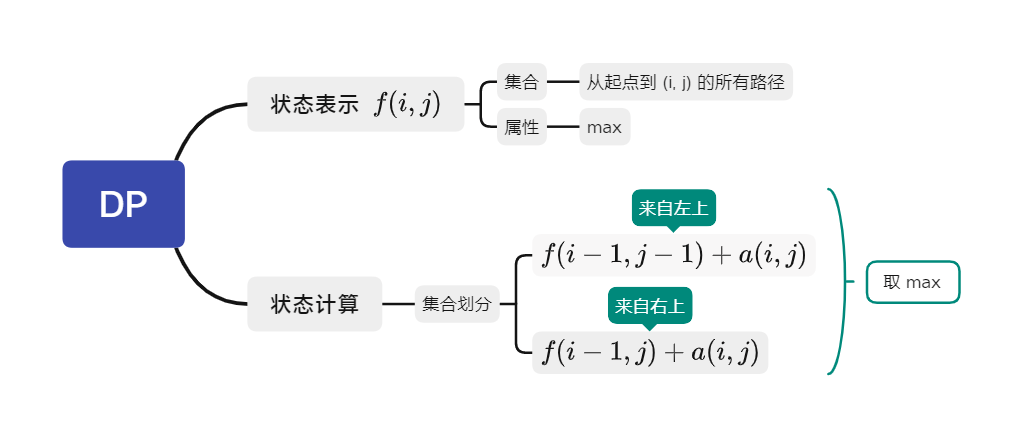
最长上升子序列
- T:895. 最长上升子序列
- DP 分析:
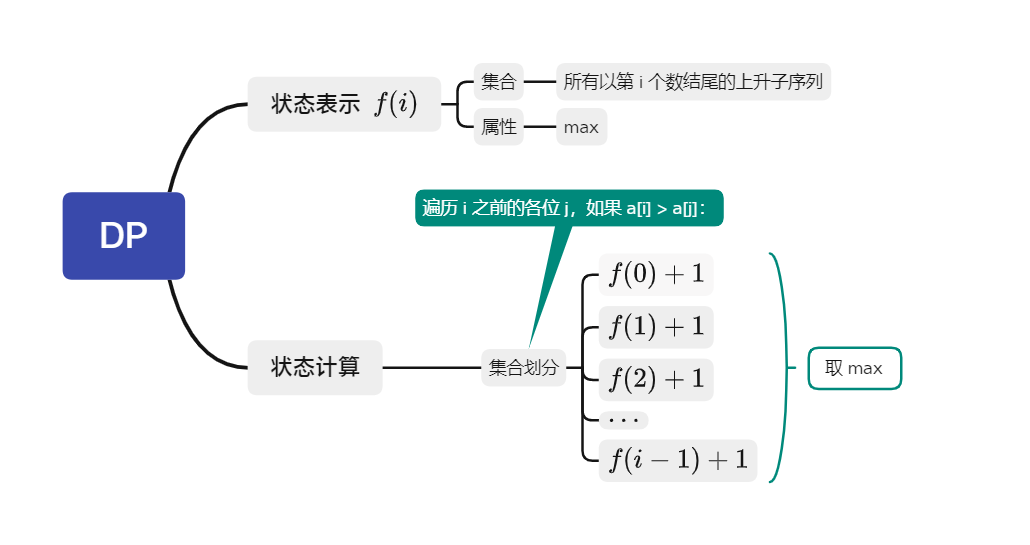
-
贪心优化:
- 二分版:
1
2
3
4
5
6
7
8
9
10
11
12
13
14int len = 0; // 最长上升子序列 q[] 长度
for (int i = 0; i < n; i ++ )
{
int l = 0, r = len;
while (l < r)
{
int mid = l + (r - l) / 2;
if (q[mid] < a[i]) l = mid;
else r = mid + 1;
}
q[r ++ ] = a[i];
len = max(len, r);
}
cout << len << endl; -
stl 版
1
2
3
4
5
6
7
8
9
10vector<int> stk; //类似于单调栈
stk.push_back(arr[0]);
for (int i = 1; i < n; i ++ ) {
if (arr[i] > stk.back())
stk.push_back(arr[i]); // 如果该元素大于栈顶元素,将该元素入栈
else
*lower_bound(stk.begin(), stk.end(), arr[i]) = arr[i]; // 替换掉第一个大于或者等于这个数字的那个数
}
cout << stk.size() << endl;
最长公共子序列
- T:897. 最长公共子序列
- DP 分析:
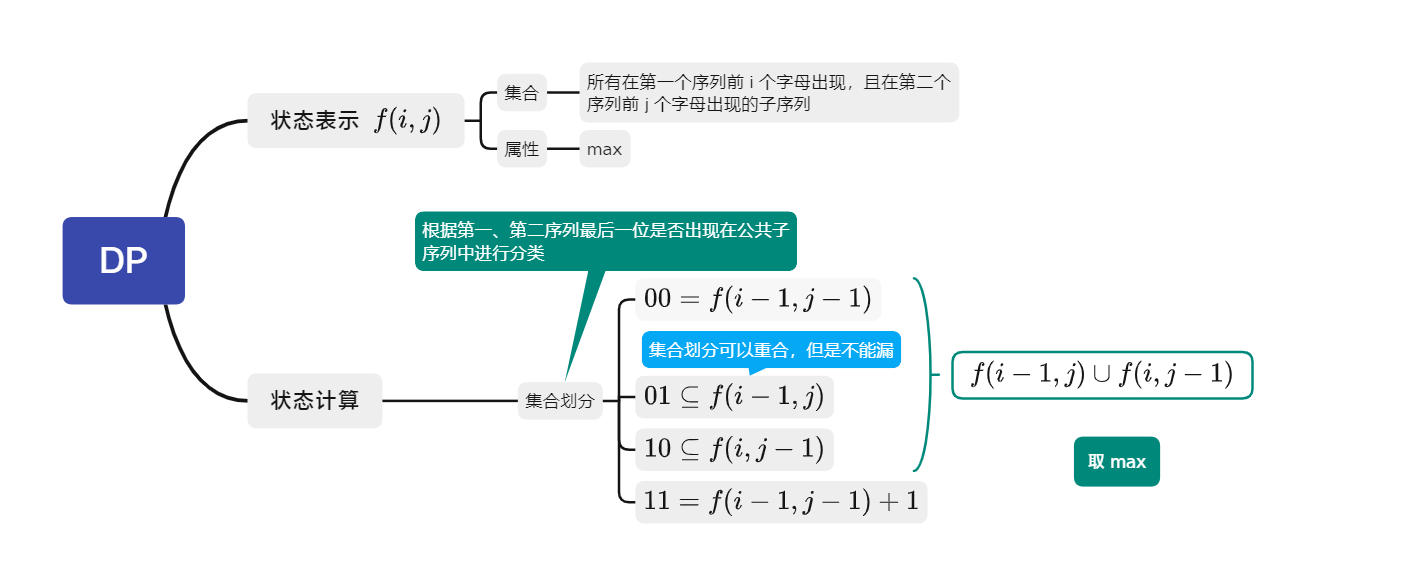
最短编辑距离
- T:902. 最短编辑距离
- DP 分析:

区间 DP
-
线性 DP 的扩展,以区间长度为阶段,使用能足够表示区间的坐标表示状态
-
特点:对整个问题设最优值,枚举合并点,将问题分解为左右两个部分,最后合并两个部分的最优值得到原问题的最优值。
-
模板
- 所有的区间 DP 问题,第一维都是枚举区间长度,一般
len = 1用来初始化,枚举从len = 2开始,第二维枚举起点i(右端点j自动获得,j = i + len - 1)
- 所有的区间 DP 问题,第一维都是枚举区间长度,一般
1 | |
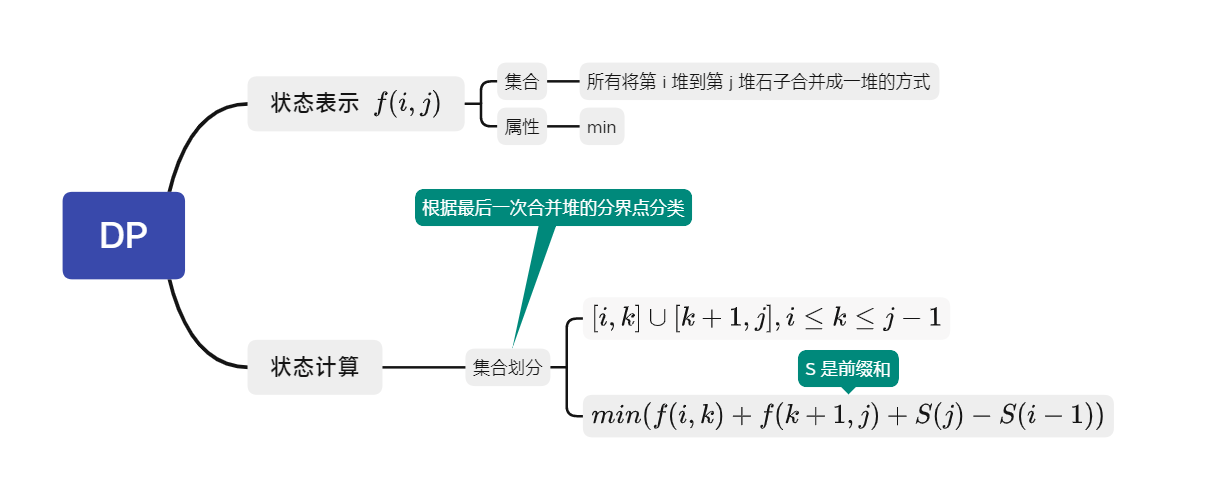
石子合并
- T:282. 石子合并
- DP 分析:
计数类 DP
整数划分
- 问题:把 拆分成 的和的方案数(不考虑顺序)
- DP 分析:
- 基于完全背包问题

- 基于“总和-个数”
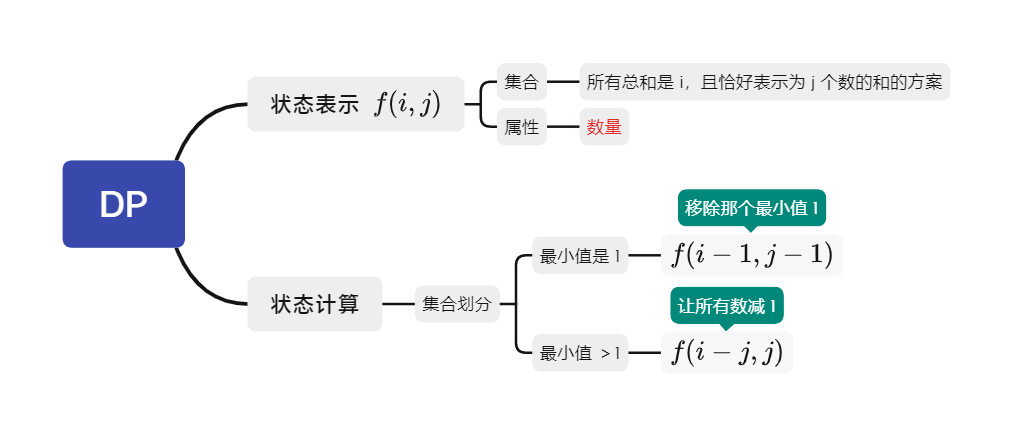
- 基于完全背包问题
数位统计 DP
- 数位:把一个数字按照个、十、百、千等等逐位拆开,关注它每一位上的数字。
- 数位 DP 的基本原理:对于位数比较多的数,这样的过程中有许多重复的部分。我们可以把这些过程归并起来,将这些过程中产生的计数答案也都存在一个通用的数组里。此数组根据题目具体要求设置状态,用递推或 DP 的方式进行状态转移。
- 数位 DP 中通常会利用常规计数问题技巧,比如把一个区间内的答案拆成两部分相减(类似于前缀和)
计算问题
- 问题:给定两个整数 和 ,求 和 之间的所有数字中 的出现次数
- 思路:实现
count(n,x),表示 中,数字 出现的次数。- 考虑 在 第四位 时出现的次数。可以将 看成
- 当 时,:
- 当 ,此时 出现了 次
- 当 ,由于 时 实际并没有第四位 ,所以此时 共出现了 次
- 当 时:
- 当 ,,此时 出现 0 次;
- 当 ,,此时 出现 次
- 当 ,,此时 出现 次
- 当 时,:
- 考虑 在 第四位 时出现的次数。可以将 看成
状态压缩 DP
- 状态压缩是通过用二进制数表示状态实现的
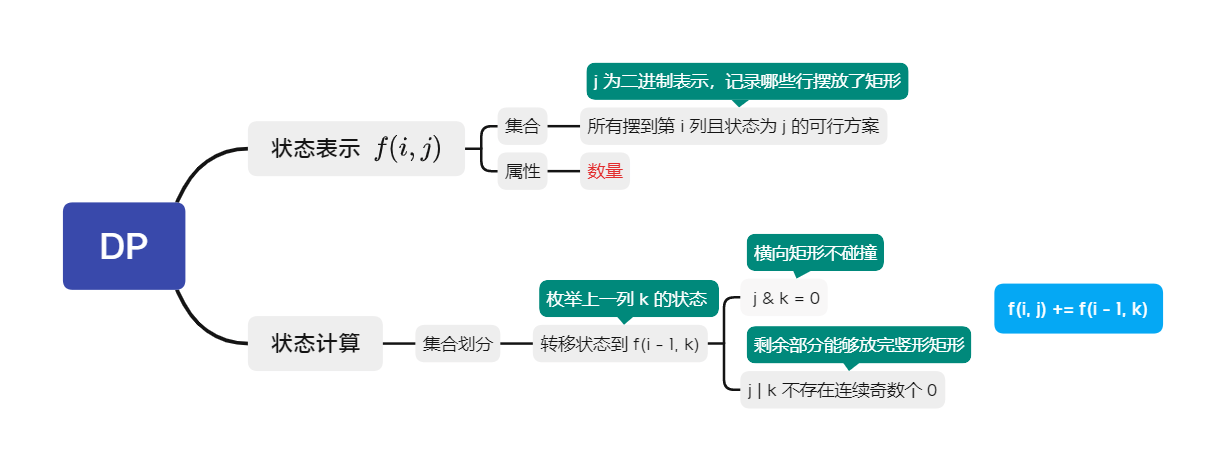
蒙德里安的梦想
- T:291. 蒙德里安的梦想
- DP 分析:
最短 Hamilton 路径
- T:91. 最短 Hamilton 路径
- DP 分析:

树形 DP
- 树形 DP:在树上进行的 DP
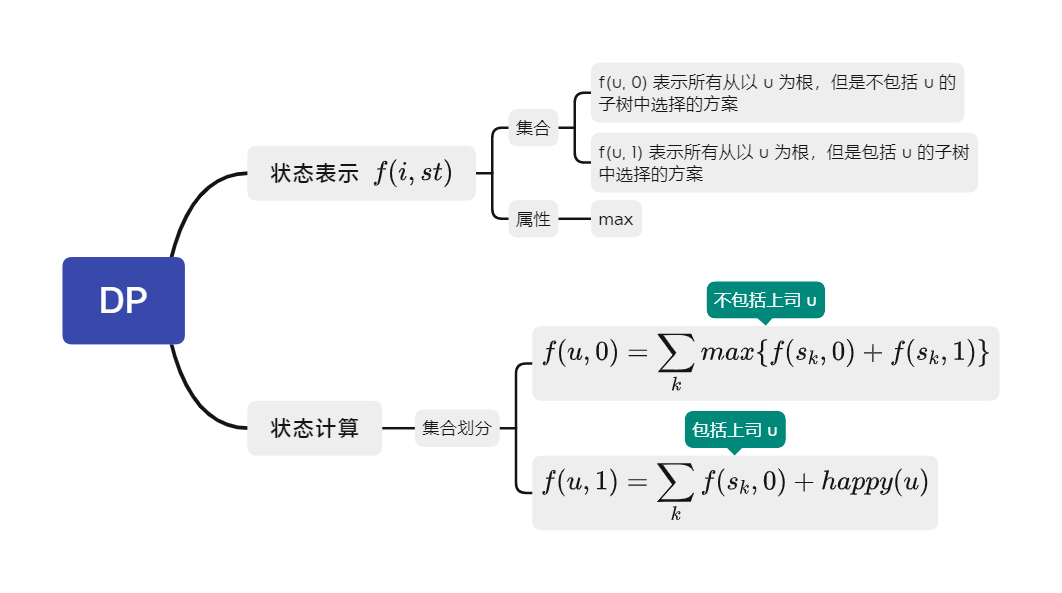
没有上司的舞会
- T:285. 没有上司的舞会
- DP 分析:
记忆化搜索
- 任何一个 DP 方程都能转为记忆化搜索。记忆化搜索的优点是特别好写,但是效率有时不如 DP 写法
- 模板
1 | |
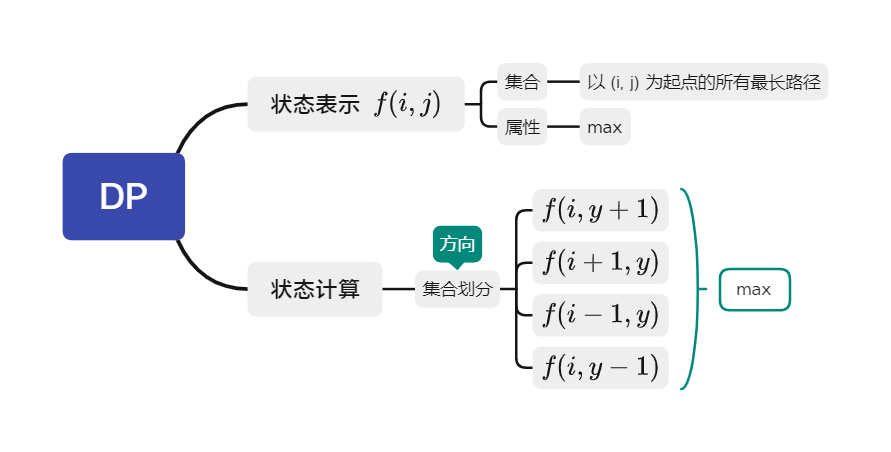
滑雪
- T:901. 滑雪
- DP 分析:
算法备忘录系列目录:
第一节 算法备忘录·基础算法
第二节 算法备忘录·数据结构
第三节 算法备忘录·杂项
第四节 算法备忘录·搜索与图论
第五节 算法备忘录·数学知识
第六节 算法备忘录·动态规划
第七节 算法备忘录·贪心
第八节 算法备忘录·时空复杂度分析
第九节 算法备忘录·杂项
算法备忘录·动态规划
https://justloseit.top/算法备忘录·动态规划/